Logistic Regression Guide
A Quick and Easy Overview of Logistic Regression
Logistic regression is a particular type of linear classifier, where the goal is to predict the probability of a binary outcome (yes/no, true/false).
Linear Classifier
A linear classifier utilies a linear function to separate classes by a line
(or a hyperplane in higher dimensions): z(x) = wx + b:
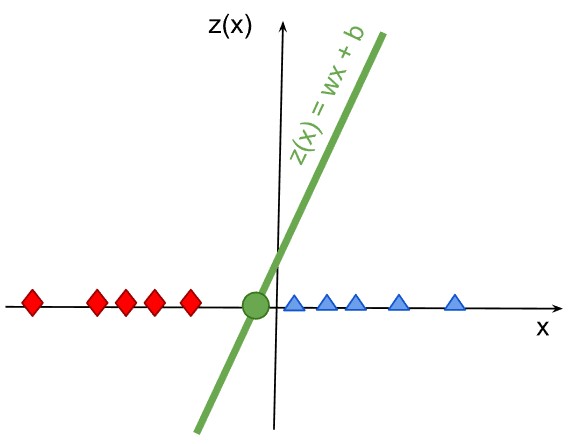
Here, w is the weight vector and b is the bias term.
Since the fuction z(x) returnes a real number in the range (-∞, +∞), we convert
this output to a class decision 'red diamond' and 'blue triangle'
by applying a threshold.
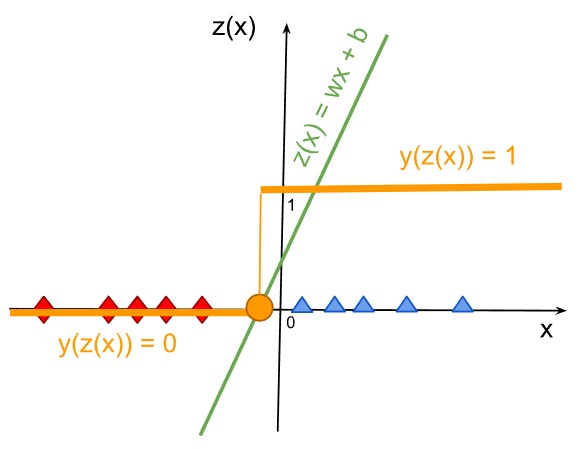
In many linear classification algorithms,
a simple threshold of 0 is commonly used to make classification decisions.:
- If
z(x) ≥ 0, then we classify as ‘red diamond’, i.g., our prediction isy = 0; - If
z(x) < 0, then we classify as ‘blue triangle’, i.g., our prediction isy = 1.
Thus, we are getting the threshold function to map the continuous
values of linear decision z(x) to binary predictions y:
Logistic Regression
Logistic regression is a particular type of linear classifier,
where we replace the simple threshold function with a sigmoid function:
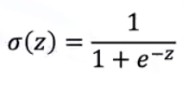
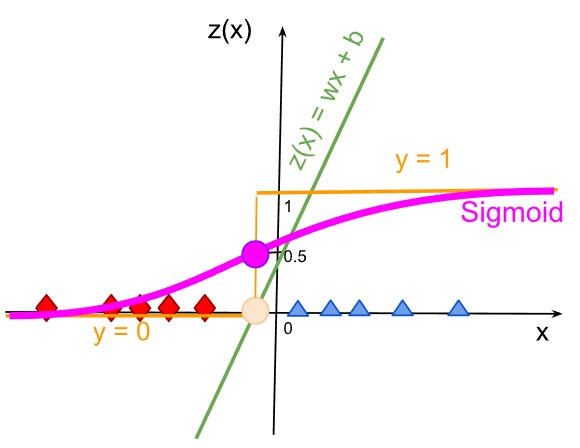
Since the sigmoid fuction returnes a real number in the range (0, 1),
we can concider this value as a confidence score for the class.
Thus:
-
If the sample point is very close to the boundary line, the output of the sigmoid function is very close to
0.5. It means, we are not certain if the class is correct. -
If the points are faraway, the outputs of sigmoid function are close to
0(‘red diamond’) or1(‘blue triangle’). Expectedly, it means, we are certain of their class.
These principles are the foundation of linear classification and logistic regression, which are widely used due to their simplicity and effectiveness in many practical applications.